Chemical Engineering

                                                                                   Steam Requirement for Evaporation

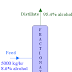
An evaporator is fed with10000 kg/hr of a solution containing 1% solute by weight. It is to be concentrated to 1.5% solute by weight. The feed is at a temperature of 37^oC. The water is evaporated by heating with steam available at a pressure of 1.34 atm absolute, corresponding to a temperature of 108.3^oC. The operating pressure in the vapor space is 1 atm absolute. Boiling point elevation and other effects can be neglected. The condensate leaves at the condensing temperature. All the physical properties of the solution may be taken to be same as that of water. What is the quantity of steam required per hour?

Data:
Enthalpy of feed = 38.1 kcal/kg
Enthalpy of solution inside the evaporator (at 100^oC) = 98 kcal/kg
Enthalpy of vapor at 100^oC = 644 kcal/kg
Latent heat of vaporization of steam = 540 kcal/kg

Calculations:

Basis: 10000 kg/hr of solution containing 1% solute by weight.

Let us denote the feed stream as F and Concentrated solution stream as P, and water evaporated as W and the concentration of solute as x

Balance on solute:

Solute in the feed = solute in the concentrated liquor

i.e., Fx = Px

10000 x 0.01 = P x 0.015

therefore, P = 6666.7 kg/hr.

and water evaporated (W) = F - P = 10000 - 6666.7 = 3333.3 kg/hr.

Enthalpy balance:

FH_F + Sl _s = WH_W + PH_P

Where, H_F = enthalpy of feed = 38.1 kcal/kg

H_W = enthalpy of water vapor = 644 kcal/kg

H_P = enthalpy of product = 98 kcal/kg

l _s = Latent heat of steam = 540 kcal/kg

therefore,

10000 x 38.1 + S x 540 = 3333.3 x 644 + 6666.7 x 98

S = 4479.6 kg/hr

i.e., steam required = 4479.6 kg/hr.

                                       
                             


 Energy Requirement for Heating

The analysis of 15000 litre of gas mixture at standard conditions is as follows:

How much heat must be added to this gas to change its temperature from 25^oC to 700^oC?

Gas  CO2 SO2 O2 N2
Cp at 25oC 8.884 9.54 7.017 6.961
Cp at 700oC 11.303 11.66 7.706 7.298

Calculations:

Basis: 15000 litre of gas

22.4 litre is occupied by 1 gmol of gas at at 0^oC.

therefore, number of gmol of gas in the volume of 15000 litre at 25^oC, is estimated as:

PV = nRT (Ideal gas equation)

From the above equation,

n₂P₁V₁/T₁ = n₁P₂V₂/T₂

here P₁ and P₂ are the same.

Therefore,

n₂ x 22.4 / 273 = 1 x 15000 / (273 + 25)

n₂ = 613.5 gmol = 0.6135 kmol

Heat required (H) to raise the temperature from 25^oC to 700^oC is given by,

H = S n_iC_Pmi(T₂ - T₁) = S n_iC_Pmi (700 - 25)

Where n_i is the moles of component 'i', and C_Pmi is the mean molal specific heat of component 'i'.

The calculations are shown in the following table.

                                                                   



                                       Solvent Recovery

A solvent recovery system delivers a gas saturated with benzene (C₆H₆) vapor that analyzes on a benzene free basis as follows: CO₂ - 15%; O₂ - 4% and N₂ - 81%. This gas is at 21^oC and 750 mm Hg pressure. It is compressed to 5 atmospheres and cooled to 21^oC after compression. How many kilograms of benzene are condensed by this process per 1000 m³ of the original mixture?

Data: Vapor pressure of benzene at 21^oC = 75 mm Hg.

Calculations:

Basis: 100 moles of Benzene free vapor.

At saturation,

p_A/(p - p_A) = p_S/(p - p_S)

where p_A is the partial pressure of benzene;

p is the total pressure of the system;

p_S is the vapor pressure of benzene at system temperature.

Therefore,

p_A = p_S = 75 mm Hg

sum of the partial pressure of benzene free gases is = 750 - 75 = 675 mm Hg.

Moles of Benzene/mole of benzene free gases at a total pressure of 750 mm Hg= 75/675 = 0.1111

At a total pressure of 5 atm ( = 5 x 760 = 3800 mm Hg),

moles of benzene per mole of benzene free gases in the gas phase = 75/(3800 - 75) = 0.0201.

The remaining moles of benzene condense into liquid phase.

Initial mole fraction of benzene in the gas mixture = 75/750 = 0.1

Partial volume of benzene in the gas mixture at the initial conditions = 0.1 x 1000 = 100 m³

Number of moles of benzene in the gas mixture at the initial conditions:

Using ideal gas equation,

P₁V₁/n₁T₁ = P₂V₂/n₂T₂

760 x 22.4/(1 x 273) = 750 x 100/(n₂ x 294)

n₂ = 4.091 kmol.

i.e., no of moles of benzene in the gas mixture = 4.0909 kmol

And the number of moles of benzene free gas in the gas mixture = 40.909 - 4.0909 = 36.8181 kmol.

Number of moles of benzene condensed

= No of moles of benzene in the gas mixture at initial conditions - at final conditions

= 4.0909 - 0.0201 x 36.8181 = 3.3509 kmol.

Mass of benzene condensed = 3.3509 x molecular weight of benzene = 3.3509 x 78 = 261.4 kg

                                                                      Extraction

A liquid containing 47.5% acetic acid and 52.5% water is to be separated by solvent extraction using isopropanol. The solvent used is 1.3 kg per kg of feed. The final extract is found to contain 82% acid on solvent free basis. The residue has 14% acid on solvent free basis. Find the percentage extraction of acid from the feed.

Calculations:

Basis: 1 kg of solvent free acid.

Acetic acid in the feed = 0.475 kg

Water in the feed = 0.525 kg

Entering acid has to come out in the extract and residue (raffinate) phases.

Let as denote the streams with the following representation.

Feed: F

Extract: E

Residue: R

Solvent: S

And the mass fractions of acetic acid (on solvent free basis) in various streams:

Acetic acid in the feed: x_F

Acetic acid in extract: x_E

Acetic acid in residue x_R

And the mass fraction of acetic acid in the solvent is zero, since the solvent is a pure one.

Balance on acetic acid:

Fx_F = Ex_E + Rx_R

1 x 0.475 = E x 0.82 + R x 0.14

0.475 = 0.82 E + 0.14 R à 1

similarly writing the balance for water,

0.525 = (1 - 0.82) E + (1 - 0.14) R

0.525 = 0.18 E + 0.86 R à 2

solving equations 1 and 2,

E = 0.493 kg, and

R = 0.507 kg.

Amount of acetic acid in the extract = 0.493 x 0.82 = 0.4043 kg.

Percentage extraction of acetic acid = 100 x Acetic acid in the extract / Acetic acid In feed

= 100 x 0.4043/0.475 = 85.12

                                                              Drying

A stock containing 1.526 kg moisture per kg dry solid is dried to 0.099 kg moisture per kg dry solid by countercurrent air flow. Fresh air entering contains 0.0152 kg water per kg dry sir and the exit air has 0.0526 kg water per kg dry air. What fraction of air is recycled if 52.5 kg of dry air flows per 1 kg of dry solid inside the drier?

Calculations:

Basis: 1 kg of dry solid

Material balance for moisture in air:

Water in stream M+ moisture added by drying of solid = Water in stream D

From the problem statement, 52.5 kg dry air is flowing per kg of dry solid and exit air is having a water content of 0.0526 kg per kg of dry air.

Therefore, water in the air leaving the dryer = 52.5 x 0.0526 = 2.7615 kg

Water added by drying of solid = 1.562 - 0.099 = 1.463 kg

Water in the stream M = 2.7615 - 1.463 = 1.2985 kg

Water in stream F + water in stream R = water in stream M

i.e.,

0.0152 F + 0.0526 R = 1.2985 à 1

and balance for dry air:

F + R = 52.5 à 2

Multiplying equation 2 with 0.0152,

0.0152 F + 0.0152 R = 0.798 à 3

subtracting equation 3 from equation 1,

0.0374 R = 0.5005

R = 13.382 kg

Substituting for R in equation 2,

F = 52.5 - 13.382 = 39.118 kg

Recycle ratio = Recycle amount / fresh feed = 13.382 / 39.118 = 0.342

                                                            Distillation

A solution of ethyl alcohol containing 8.6% alcohol by weight is fed at the rate of 5000 kg/hr to a continuous fractionating column operating at atmospheric pressure. The distillate which is the desired product contains 95.4% alcohol by weight and the residue from the bottom of the column contains 0.1% alcohol by weight. Calculate the following:

Calculations:

Overall material balance:

Feed = Distillate + Residue

i.e., F = D + R

D + R = 5000 à 1

Component balance for Alcohol:

Fx_F = Dx_D + Rx_R

Where x 's are the mole fraction of alcohol in various streams.

0.954 D + 0.001 R = 5000 x 0.086 = 430 à 2

Equations 1 and 2 contains 2 unknowns D and R, and that can be solved as follows:

Multiplying equation 1 by 0.001,

0.001D + 0.001 R = 5 à 3

subtracting equation 3 from equation 2,

0.953 D = 425

D = 446 kg/hr

i.e., Distillate flow rate = 446 kg/hr

Therefore, R = 5000 - 446 = 4554 kg/hr

i.e., Residue flow rate = 4554 kg/hr

Ethanol leaving in the residue (i.e., ethanol lost) = 4554 x 0.001 = 4.554 kg/hr

Ethanol entering in the feed = 5000 x 0.086 = 430 kg/hr

Percentage loss of ethanol = 100 x (4.554 / 430) = 1.06

                                                             Evaporation

An evaporator is fed continuously with 25 kg/hr of a solution which contains 10% NaCl, 10% NaOH and 80% H₂O. During evaporation, H₂O is removed from the solution and NaCl precipitates as crystals which is settled and removed. The concentrated liquor leaving the evaporator contains 50% NaOH, 2% NaCl and 48% H₂O. Calculate

Calculations:

Data:

Flow rate of feed = 25 kg/hr

Composition of feed (F):

NaCl 10%

NaOH 10%

H₂O 80%

Composition of concentrated liquor (P):

NaCl 2%

NaOH 48%

H₂O 50%

Balance for NaOH:

NaOH entering the in feed = NaOH leaving in concentrated liquor

i.e., 0.1 x 25 = 0.50 P

Therefore, the mass flow rate of concentrated liquor (P) = 0.1 x 25 / 0.50 = 5 kg/hr

Balance for NaCl:

NaCl entering in the feed = 25 x 0.1 = 2.5 kg/hr

The entering NaCl is coming out as crystals and in the concentrated liquor.

NaCl leaving in the concentrated liquor = 0.02 P = 0.02 x 5 = 0.1 kg/hr

Therefore,

NaCl precipitated = 2.5 - 0.1 = 2.4 kg/hr